题目描述:请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 ‘1’。示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 ‘1’。
1 | public class Solution { |
方法一:诸位判断
利用 与运算 的特点,设二进制数字 n ,则有:
- 若 n & 1 = 0 ,则 n 二进制 最右一位 为 0 ;
- 若 n & 1 = 1 ,则 n 二进制 最右一位 为 1 。
根据以上特点,考虑以下 循环判断 :
- 判断 n 最右一位是否为 1 ,根据结果计数。
- 将 n 右移一位(本题要求把数字 n 看作无符号数,因此使用 无符号右移 操作)。
1 | public class Solution { |
复杂度分析:
- 时间复杂度:O(log2n),此算法循环内部仅有 移位、与、加 等基本运算,占用 O(1) ;逐位判断需循环 log2n 次,其中 log2n 代表数字 n 最高位 1 的所在位数(例如 log24 = 2, log216 = 4)
- 空间复杂度:O(1),变量 res 使用常数大小额外空间
执行结果:通过
执行用时:1 ms, 在所有 Java 提交中击败了99.27%的用户
内存消耗:36.8 MB, 在所有 Java 提交中击败了22.62%的用户
方法二:巧用 n&(n-1)
(n−1) 解析: 二进制数字 n 最右边的 1 变成 0 ,此 1 右边的 0 都变成 1
n&(n−1) 解析: 二进制数字 n 最右边的 1 变成 0 ,其余不变
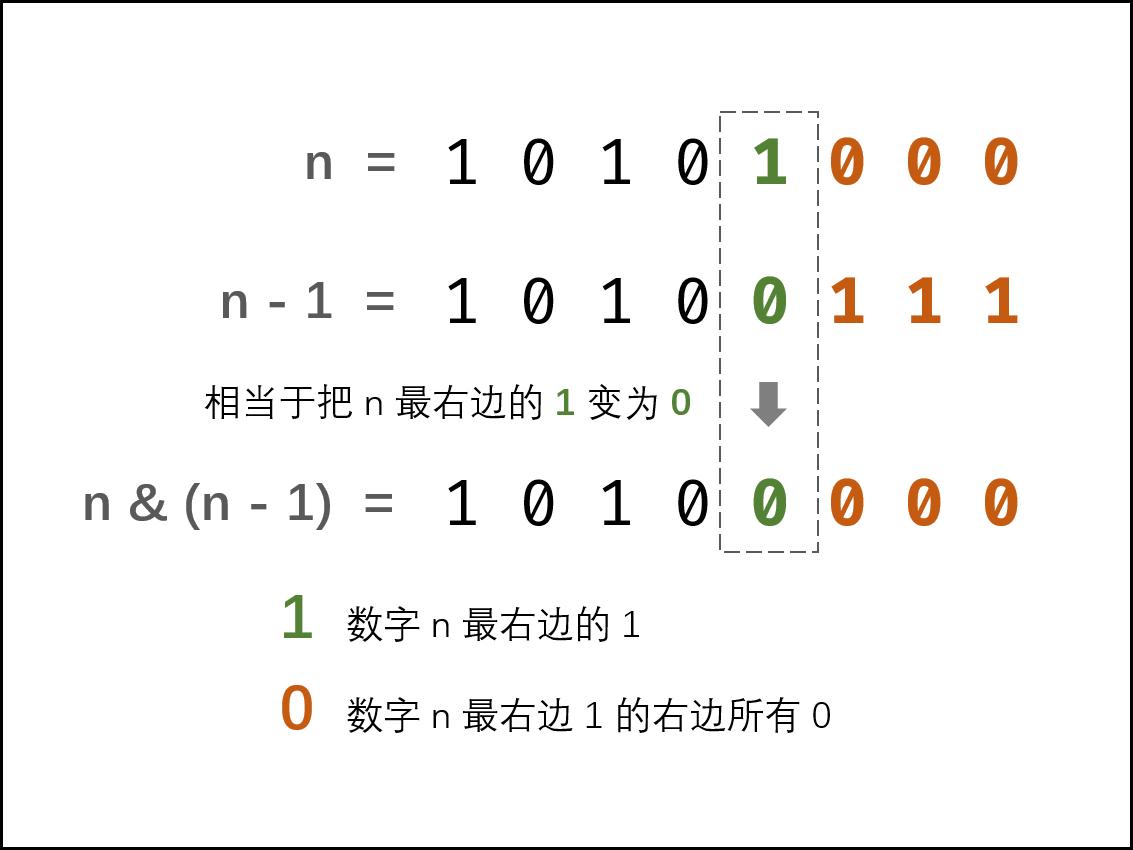
要领:循环消除 n 最右边的 1,并计算
1 | public class Solution { |
复杂度分析:
- 时间复杂度:O(M),n & (n - 1) 操作仅有减法和与运算,占用 O(1) ;设 M 为二进制数字 n 中 1 的个数,则需循环 M 次(每轮消去一个 1 ),占用 O(M)
- 空间复杂度:O(1),变量 res 使用常数大小额外空间
执行结果:通过
执行用时:1 ms, 在所有 Java 提交中击败了99.27%的用户
内存消耗:36.6 MB, 在所有 Java 提交中击败了72.04%的用户